量子动力学(02):一维线性势与 WKB 近似
线性势是经典重力场或者匀强电场的对应, 本节介绍一维线性势下的严格解, 以及一类非常有用的半经典近似——WKB近似.\(\newcommand{\K}{\mathbb{K}}\newcommand{\R}{\mathbb{R}}\newcommand{\C}{\mathbb{C}}\newcommand{\b}{\mathbf}\newcommand{\bi}{\boldsymbol}\newcommand{\rank}[1]{\text{rank}\left(#1 \right)}\newcommand{\dim}[1]{\text{dim}\left(#1 \right)}\newcommand{\diag}[1]{\text{diag}\left(#1 \right)}\newcommand{\det}[1]{\text{det}\left(#1 \right)}\newcommand{\Det}[1]{\left|\begin{matrix} #1 \end{matrix}\right|}\newcommand{\set}[1]{\left\{ #1 \right\}}\newcommand{\abs}[1]{\left| #1 \right|}\newcommand{\norm}[1]{\left|\!\left|#1\right|\!\right|}\)
一维线性势场下的本征态
所谓线性势, 就是满足\(V(x)=kx\)形式的势场. 当然, 无论是经典还是量子力学, 都需要作一点小小的修正, 例如引入刚性边界或者设置为\(V(|x|)\), 否则, 经典粒子会无限下坠, 量子在\(-\infty\)处会具有无限大的波矢. 总而言之, 我们所说的线性势问题中的运动方程为 \[ -\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}+kx\psi(x)=E\psi(x)\quad x\ge0 \] 为了很好地解出这个方程, 需要两步操作, 第一步是无量纲化: \[ x_0=\sqrt[3]{\frac{\hbar^2}{mk}}\qquad y=x/x_0\quad \varepsilon=\frac{E}{kx_0} \] 于是无量纲化的定态 Schrodinger 方程为 \[ \frac{d^2}{dy^2}\psi=2(y-\varepsilon)\psi \] 第二步是将它转化为我们更加熟悉的数学物理方程, 令\(z=\left(2(\varepsilon-y) \right)^{3/2}/3\), \(\psi=\sqrt{\varepsilon-y}u\), 则 \[ \begin{aligned} \frac{d\psi}{dy}&=\frac{dz}{dy}\frac{d}{dz}(\sqrt{y}u)=\frac{u+3zu'}{\sqrt{2}(3z)^{1/3}} \\ \frac{d^2\psi}{dy^2}&=(3z)^{1/3}\frac{d}{dz}\left[\frac{u+3zu'}{\sqrt{2}(3z)^{1/3}}\right]=\frac{9z^2u''+9zu'-u}{3\sqrt{2}z} \\ 2(y-\varepsilon)\psi&=-\frac{3z}{2^{3/2}}\cdot2u=-\frac{3zu}{\sqrt{2}} \end{aligned} \] 整理得 \[ z^2 u''+zu'+(z^2-\frac{1}{9})u=0 \] 这是\(1/3\)阶 Bessel 方程, 它的解可以表示为相应阶和相反阶的 Bessel 函数的线性组合.
经典禁区
在经典禁区(\(y>\varepsilon\)), \(z\)是纯虚数, 应该改用\(iz\)为宗量, 解应该改用第一、二类变型 Bessel 函数. 即 \[ \psi=A \zeta^{1/3} I_{1/3}(\zeta)+B\zeta^{1/3} K_{1/3}(\zeta)\quad \zeta=\frac{[2(y-\varepsilon)]^{3/2}}{3} \] 考虑到无穷远处\(\psi\)应当收敛为\(0\), \(I_{1/3}(+\infty)\)会发散, 应当舍去. 即 \[ \psi=B\zeta^{1/3}K_{1/3}(\zeta) \]
经典允许区
经典允许区的范围是\(0<y<\varepsilon\), 此时\(z\)是正实数, 可以直接用\(J_{1/3}(z)\)和\(J_{-1/3}(z)\)的线性组合表示波函数. 考虑到此处与禁区的光滑连接, 可以对禁区波函数作解析延拓: \[ \begin{aligned} \psi&=B(iz)^{1/3}\frac{I_{-1/3}(iz)-I_{1/3}(iz)}{\frac{2}{\pi}\sin\frac{\pi}{3}} \\&=B(iz)^{1/3}\frac{i^{1/3}J_{-1/3}(-z)-i^{-1/3}J_{1/3}(-z)}{\frac{2}{\pi}\sin\frac{\pi}{3}} \\&=\frac{\pi Bz^{1/3}}{\sqrt{3}}(-i^{2/3}J_{-1/3}(z)+J_{1/3}(z)) \end{aligned} \] 由于禁区波函数\(\psi\)是纯实的(不考虑\(B\)), 因此这里也应取作纯实数, \(i^{2/3}\)作为一个多值函数的值(\(\exp(\frac{4n+1}{3}\pi)\)), 唯一的实值是\(-1\), 因此 \[ \psi=\frac{\pi B}{\sqrt{3}}z^{1/3}(J_{1/3}(z)+J_{-1/3}(z)) \]
能级
经典允许区另一个端点\(y=0\)(\(z=(2\varepsilon)^{3/2}/3\))也给出边界条件. 由于\(y<0\)部分被取作无限高势垒, 波函数只允许奇宇称, 原点处函数值为\(0\). 即 \[ J_{1/3}((2\varepsilon)^{3/2}/3)+J_{-1/3}((2\varepsilon)^{3/2}/3)=0 \] 所有严格能级都是上式的解. 对于\(\varepsilon\gg1\)的情形, 可以利用 Bessel 函数的展开: \[ J_\alpha(x)\sim\frac{\cos(x-\frac{2\alpha+1}{4}\pi)}{\sqrt{x}} \] 代入可得 \[ \frac{(2\varepsilon)^{3/2}}{3}=(n+\frac{3}{4})\pi\Rightarrow E=\sqrt[3]{\frac{\hbar^2k^2}{2m}}\left[\frac{3\pi}{2}(n+\frac{3}{4}) \right]^{2/3}\quad n\gg1 \]
WKB 近似
求解了线性势问题之后, 引进一种称为 WKB 近似的方法是很值得花些时间的. 写出如下定态 Schrodinger 方程 \[ -\frac{\hbar^2}{2m}\nabla^2\psi=(E-V)\psi \] 定义波矢函数 \[ k(x):=\sqrt{\frac{2m(E-V(x))}{\hbar^2}} \] 并且将波函数改写为如下形式[1] \[ \psi=\exp(\frac{i W(x)}{\hbar}) \]
代入可得 \[ \left(\frac{d W}{dx}\right)^2-i\hbar\frac{d^2W}{dx^2}=\hbar^2k(x)^2 \] 如果\(k(x)\)是个与位置无关的常量, 显然\(W=\hbar\vec{k}\cdot\vec{r}+C\), 二阶导严格为\(0\); 现在考虑\(k(x)\)在空间中构成非均匀标量场, 但它在空间中是如此缓慢变化, 以至于\(W(x)\)也随之缓慢变化: \[ \hbar\frac{d^2 W}{dx^2}\ll\left(\frac{dW}{dx}\right)^2 \] 基于这个条件可以计算微分方程的微扰解, 零阶项完全舍去了\(W''\): \[ W_0'(x)=\pm\hbar k(x) \] 一阶项: \[ (W_0'+W_1')^2=\hbar^2k(x)^2+i\hbar W_0'' \] 只使用前两阶项作为最终结果, 得到 \[ W=\int^x dx'(W_0'(x')+W_1'(x'))=\pm\int^xdx'\hbar\sqrt{k(x')^2\pm ik'(x')} \] 应当注意到\(k(x)\)随位置缓慢变化, 因此 \[ W(x)\approx\pm\int^xdx'\hbar(k(x')\pm\frac{ik'(x')}{2k(x')})=\frac{i\hbar}{2}\log(k(x))\pm \int^xdx'\hbar k(x') \] 代入波函数, 得到 \[ \psi(x)\sim\frac{\exp({\displaystyle\pm i\int^xk(x')dx'})}{\sqrt[4]{E-V(x)}} \] 这就是 WKB 近似(Wentzel-Kramers-Brillouin approximation). 接下来我们将运用 WKB 近似讨论不同势场形状下的结论.
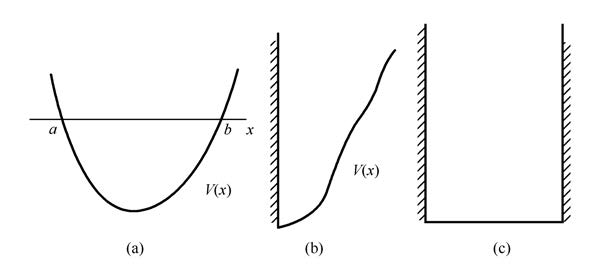
类简谐势场的束缚态
考虑一个一维势场, 它具有如下条件:
- 势函数\(V(x)\)处处连续, 且\(V(\pm\infty)=+\infty\);
- 所有能量本征值均能取到且仅取到两个转折点\(x_1,x_2\)(\(x_1<x_2\)), 即\(x_1<x<x_2\)时是经典允许区, \(x<x_1\)或\(x>x_2\)时是经典禁区.
这种势没有特定的名字, 简单的例子是简谐势, 因此直接称为"类简谐势场". 允许区的波函数使用 WKB 近似的结果线性组合成实函数得到 \[ \psi_L=\frac{\cos(\int^x_{x_1}k(x')dx'-\frac{\pi}{4})}{\sqrt[4]{E-V(x)}} \]
Remark
此处的\(\pi/4\)相位来自线性势的解. 类简谐势场在转折点附近总可以近似为线性势, 则经典允许区的解为 \[ \psi\sim J_{1/3}(z)+J_{-1/3}(z) \] 取\(z\rightarrow\infty\), 这里的无穷大对于缓变函数\(V(x)\)来说其实很小, 不足以破坏线性势近似; 但对于 Bessel 函数来说很大, 可以利用渐近展开取近似, 其三角函数部分正是\(\cos(z-\pi/4)\).
另一方面, 对于右转折点, 同样可以得到一个近似结果 \[ \psi_R=\frac{\cos(\int_x^{x_2}k(x')dx'-\frac{\pi}{4})}{\sqrt[4]{E-V(x)}} \] \(\psi\)是单值函数, 三角函数部分相等; 但它们宗量的差显然不是定值, 而和是定值, 因此宗量和一定是\(n\pi\) \[ \int_{x_1}^{x_2} k(x)dx=\left(n+\frac{1}{2} \right)\pi \] 了解量子力学史或者旧量子论的人应当对上式感到熟悉, 改写成动量形式, 并且积分一个周期(这意味着\(x_1,x_2\)之间一来一回), 正是 Sommerfeld 量子化条件: \[ \boxed{\oint p(x)dx=\left(n+\frac{1}{2}\right)h}\quad n=0,1,\cdots \]
类线性势场的束缚态
"类线性势场"的条件是: \(V(x)\)处处连续, 一侧在有限远\(x_1\)处变为无限高势垒, 另一侧在无限远处发散; 所有能量本征值取到一个转折点\(x_2\), \(x_1<x<x_2\)是经典允许区, \(x>x_2\)是经典禁区.
这种势场在\(x_1\)处相当于具有间断点, 因此取值为\(0\); 在\(x_2\)处仍类似前述讨论, 因此 \[ \psi_L\sim\cos(\int^x_{x_1}k(x')dx'-\frac{\pi}{2})\quad\psi_R\sim\cos(\int_{x}^{x_2}k(x')dx'-\frac{\pi}{4}) \] 不难证明, 对应的 Sommerfeld 量子化条件为 \[ \boxed{\oint p(x)dx=\left(n+\frac{3}{4}\right)\hbar} \]
类无限深方势阱的束缚态
"类无限深方势阱"的条件是: \(V(x)\)处处连续, 两侧均在有限远\(x_1,x_2\)处变为无限高势垒, 所有能量本征值不能取到转折点, \(x_1<x<x_2\)是经典允许区, 此外是经典和量子共同的禁区.
类似的 WKB 近似波函数和 Sommerfeld 量子化条件为 \[ \psi_L\sim\cos(\int^x_{x_1}k(x')dx'-\frac{\pi}{2})\quad\psi_R\sim\cos(\int_{x}^{x_2}k(x')dx'-\frac{\pi}{2}) \]
\[ \boxed{\oint p(x)dx=(n+1)\hbar} \]
- 了解过分析力学的 Hamilton-Jacobi 方法之后应该对此感到熟悉. ↩︎