自旋与二级相变(03)：二维 Ising 模型的渐近展开

对于更高维的 Ising 模型, 解析求解任意外场的配分函数是困难的. 针对零外场的二维 Ising 模型, 人们发展出了两种渐近展开的方法, 分别在零温和无穷高温附近适用.\(\newcommand{\K}{\mathbb{K}}\newcommand{\R}{\mathbb{R}}\newcommand{\C}{\mathbb{C}}\newcommand{\b}{\mathbf}\newcommand{\bi}{\boldsymbol}\newcommand{\rank}[1]{\text{rank}\left(#1 \right)}\newcommand{\dim}[1]{\text{dim}\left(#1 \right)}\newcommand{\diag}[1]{\text{diag}\left(#1 \right)}\newcommand{\det}[1]{\text{det}\left(#1 \right)}\newcommand{\Det}[1]{\left|\begin{matrix} #1 \end{matrix}\right|}\newcommand{\set}[1]{\left\{ #1\right\}}\newcommand{\abs}[1]{\left| #1 \right|}\newcommand{\norm}[1]{\left|\!\left|#1\right|\!\right|}\)

低温展开

可以想象, 严格零温的系统处在完全有序态, 即自旋要么全部向上, 要么全部向下. 如果偏离零温一点呢? 系统仍有较高概率处在完全有序态, 也有小概率产生一定的激发, 表现为偶尔出现一些与整体自旋取向不同的格点.

为了简化, 令\(K=\beta J\). 则系统的配分函数为 \[ Z=\sum_{\{\sigma_j\}}\exp(K\sum_{<ij>}\sigma_i\sigma_j) \] 取四角晶格, 能量较低的一些状态示意图如下.

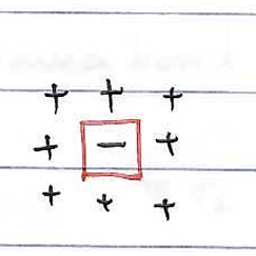
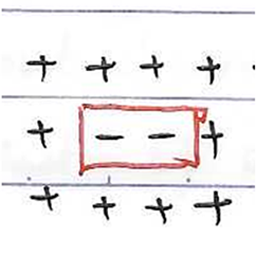
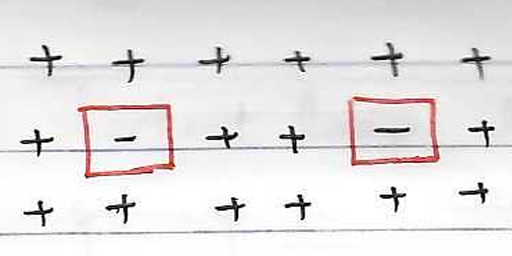
低温展开下的配分函数具体表达式为 \[ Z=2e^{2NK}\left(1+Ne^{-8K}+2Ne^{-12K}+\frac{N(N+9)}{2}e^{-16K}+\cdots\right) \]

高温展开

配分函数的另一种形式为 \[ Z=\sum_{\{\sigma_j\}}\exp(K\sum_{<ij>}\sigma_i\sigma_j)=\sum_{\{\sigma_j\}}\prod_{<ij>}\cosh(K\sigma_i\sigma_j)+\sinh(K\sigma_i\sigma_j) \] 注意到\(\sigma_i\sigma_j=\pm1\), 因此 \[ Z=\sum_{\{\sigma_j\}}\prod_{<ij>}\cosh K+\sigma_i\sigma_j\sinh K=2^N\cosh^{2N} K\sum_{\{\sigma_j\}}\prod_{<ij>}\left(1+\sigma_i\sigma_j\tanh K\right) \] 数学上取\(K=0\)表示无穷高温, 对应的配分函数为\(2^N\cosh^{2N}K\), 它代表自旋取向相互独立且完全随机. 稍稍偏离无穷高温时, \(K\ll1\), 需要将后面的连乘项作展开: \[ \frac{Z}{2^N\cosh^{2N}K}=1+\tanh K\sum_{\{\sigma_j\}}\sum_{<ij>}\sigma_i\sigma_j +\tanh ^2K\sum_{\{\sigma_j\}}\sum_{<ij>, <jk>}\sigma_i\sigma_j^2\sigma_k + \cdots \] 它非常像集团展开. 我们同样可以根据出现的自旋对绘制一些边, 上式中, 一次项\(\sigma_i\sigma_j\)代表一条边构成的图, 二次项\(\sigma_i\sigma_j^2\sigma_k\)代表两条共顶点的边构成的图, \(\sigma_i\sigma_j\sigma_k\sigma_l\)代表两条不相连的边构成的图, 以此类推. 代数上\(\sigma_j\)出现了次数的奇偶性, 代表了几何图中这个点的连通度.

和集团展开不同的是, 系数中任何\(\sigma\)的奇数次项都会被 cancel, 因为\(\sigma_j\)会取\(\pm1\)然后求和. 想要有非零贡献, 当且仅当每个\(\sigma\)都是偶数次项, 而偶数次可以约化为\(2\)次, 每个自旋的次数都是\(2\), 说明这张图中的边构成了一个闭合回路. 当然, 事实上要求更宽松, 一张合法的图总可以分解为若干个闭合回路, 并且存在分解方法使得回路之间只共顶点不共边.

基于上述讨论, 最低阶非零项对应单个最小闭合回路, 长度为\(4\); 由于四角晶格中, 任何闭合回路都可以通过平移补全为矩形, 因此长度总是偶数, 这样还存在次数为\(6, 8,\cdots\)的项.

展开图

用一些和低温展开示例类似的闭合回路来说明高温展开, 如下所示.

高温展开图示例

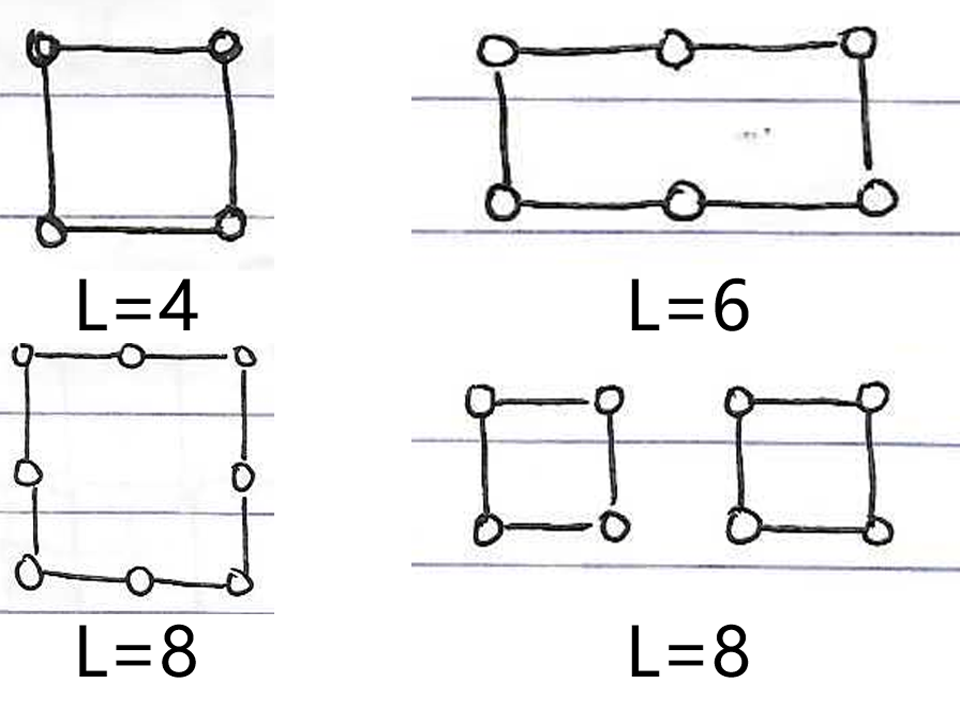
1. \(L=4\): 只有一种(如图), 考虑左上角点位置不同, 简并度为\(N\).

2. \(L=6\): 形状有一种, 分为长边横向(如图)和长边纵向两类, 每一类简并度为\(N\), 共\(2N\).

3. \(L=8\): 形状上有四种

   1. 第一种是\(2\times2\)正方形(如图), 简并度为\(N\);
   2. 第二种是两个不共边的最小回路(如图, 相对位置可变). 放下第一个正方形(左上角点\(A\)标记位置)后, 第二个正方形\(A'\)不能放在\(A\)的最近邻点(否则共边)或者\(A\)本身(否则重合), 简并度为\(N(N-5)/2\);
   3. 第三种(未画出)是\(1\times3\)矩形, 考虑长边可以放在横向或纵向, 简并度为\(2N\);
   4. 第四种(未画出)从\(2\times2\)正方形演变而来, 把它的一个顶角折到中心, 构成"楼梯状", 用正方形中心标记位置, 并且考虑缺口取向有四类, 简并度为\(4N\).

   综上, \(L=8\)简并度为\(N(N+9)/2\).

为什么不能把大正方形的两个对角都折叠到中心, 这样得到的图也是合法的? 因为这样相当于两个小正方形具有对顶角, 已经包含在第二种了.

这样, 可以写出包含前四个最低阶的展开式: \[ Z=2^N\cosh^{2N} K\left(1+N\tanh^4K+2N\tanh^6 K +\frac{N(N+9)}{2}\tanh^8 K+\cdots\right) \]

晶格的自对偶性

可以把低高温展开式整理到下面: \[ \begin{aligned} Z(K)&=2e^{2NK}\left(1+Ne^{-8K}+2Ne^{-12K}+\frac{N(N+9)}{2}e^{-16K}+\cdots\right) \\ \Xi(\kappa)&=2^N\cosh^{2N}\kappa\left(1+N\tanh^4\kappa+2N\tanh^6\kappa +\frac{N(N+9)}{2}\tanh^8\kappa+\cdots\right) \end{aligned} \] 我们发现它们具有极高的相似性. 如果强令 \[ \tanh\kappa= e^{-2K}\quad\cosh\kappa=\frac{1}{\sqrt{1-e^{-4K}}}\quad\sinh\kappa=\frac{e^{-2K}}{\sqrt{1-e^{-4K}}} \] 则\(\Xi(\kappa)\)零阶项可以用\(K\)表为 \[ 2^N\cosh^{2N}\kappa=\left(\frac{2}{1-e^{-4K}}\right)^N=\left(\frac{e^{2K}}{\sinh2K}\right)^N \] 即 \[ \Xi[\kappa(K)]/Z(K)=\frac{1}{2\sinh^{2N}2K} \] 类似地, 也可以用高温参量\(\kappa\)表示低温参量\(K\) \[ \tanh K=\frac{1-e^{-2K}}{1+e^{-2K}}=\frac{1-\tanh\kappa}{1+\tanh\kappa}=\frac{\cosh\kappa-\sinh\kappa}{\cosh\kappa+\sinh\kappa}=e^{-2\kappa} \] 通过这个式子也能推导出另两个双曲函数 \[ \cosh K=\frac{1}{\sqrt{1-e^{-4\kappa}}}\quad\sinh K=\frac{e^{-2\kappa}}{\sqrt{1-e^{-4\kappa}}} \] 两个参量的换算关系正反形式完全一样. 而对应的配分函数比值: \[ Z[K(\kappa)]/\Xi(\kappa)=2^{N+1}\sinh^N K\cosh^NK=2\left(\frac{2e^{-2\kappa}}{1-e^{-4\kappa}}\right)^N=\frac{2}{\sinh^{2N}2\kappa} \] 比较可得 \[ \sinh 2K\sinh2\kappa=1 \] 这些方程说明了二维四角晶格上的 Ising 模型具有 自对偶性(self-duality), 由上式联系起来的高温参量\(\kappa\)和低温参量\(K\)具有相似的展开式. 临界点的特点是关联长度发散, 那么

• 高温展开中很长的闭合回路贡献也不能忽略, 高温展开发散;
• 低温展开中容易形成面积很大的磁畴, 低温展开发散.

即\(\sinh 2K\sinh 2\kappa=1\), 且\(K=\kappa=\beta_c J\). 解得 \[ \boxed{T_c=\frac{2J}{k_B\log(\sqrt{2}+1)}} \] 利用自对偶性, 我们没有仔细计算配分函数和热力学量, 就得到了严格的临界温度.