经典流体(02):实际气体的集团展开
实际气体的有关概念
\(\newcommand{\K}{\mathbb{K}}\newcommand{\R}{\mathbb{R}}\newcommand{\C}{\mathbb{C}}\newcommand{\b}{\mathbf}\newcommand{\bi}{\boldsymbol}\newcommand{\rank}[1]{\text{rank}\left(#1 \right)}\newcommand{\dim}[1]{\text{dim}\left(#1 \right)}\newcommand{\diag}[1]{\text{diag}\left(#1 \right)}\newcommand{\det}[1]{\text{det}\left(#1 \right)}\newcommand{\Det}[1]{\left|\begin{matrix} #1 \end{matrix}\right|}\newcommand{\set}[1]{\left\{ #1 \right\}}\newcommand{\abs}[1]{\left| #1 \right|}\newcommand{\norm}[1]{\left|\!\left|#1\right|\!\right|}\)理想气体是实际气体的高温稀薄极限, 真正的气体只是近似满足理想的状态方程. 一般来说, 实际气体从字面上就是指"所有现实中的气体", 但对于临近相变或临界点的稠密气体, 以理想气体为出发点作逐级近似未免过于复杂和不便, 所以我们希望讨论的对象是稍加偏离理想状态的气体. 此外还有一些约定:
- 组分是全同的单原子分子, 多原子分子的其余自由度的处理方法, 此前已经讨论过;
- 分子间相互作用是两体相互作用, 并且是有心势, 只与距离有关, 与任何空间取向无关.
- 这个有心势是一种短程相互作用, 以至于系统可以看作带有微扰的近独立子系.
第三点其实和"稍加偏离理想状态"类似, 都是希望从理想气体出发逐级展开. 分子间相互作用(化学家常称为 Van der Waals 相互作用)的常见经验公式是 Lennard-Jones 势: \[ \phi(r_{ij})=4\epsilon\left[\left(\frac{\sigma}{r_{ij}} \right)^{12}-\left(\frac{\sigma}{r_{ij}} \right)^6\right] \] 它恰恰是满足上述要求的势能.
位形积分
先计算正则配分函数 \[ \begin{aligned} Z(N)&=\frac{1}{N!h^{3N}}\int\prod_j\exp(-\frac{\beta p_j^2}{2m})d^3\vec{p}_j\int\prod_{i<j}\exp(-\beta\phi(r_{ij}))\prod_jd^3\vec{r}_j \\&= \left(\frac{2\pi m}{\beta h^2}\right)^{\frac{3}{2}N}\frac{1}{N!}\int\prod_{i<j}\exp(-\beta\phi(r_{ij}))\prod_jd^3\vec{r}_j \end{aligned} \] 定义
位形积分 \[ Q_N:=\frac{1}{N!}\int\prod_{i<j}\exp(-\beta\phi(r_{ij}))\prod_jd^3\vec{r}_j \]
并引入热波长, 可以充分简化正则配分函数和巨配分函数 \[ \begin{aligned} Z(N)&=\frac{Q_N}{\lambda_T^{3N}} \\ \Xi&=\sum_N\left(\frac{e^{-\alpha}}{\lambda_T^3}\right)^NQ_N \end{aligned} \]
势能部分的展开
现在全部工作变成求解位形积分. 从微扰的角度出发, 似乎应该作 Taylor 展开 \[ \exp(-\beta\phi)=1-\beta\phi+\frac{\beta^2}{2}\phi^2+\cdots \] 问题是, \(\phi\)在力程以内很大, 这个展开能收敛于原函数上, 但收敛速度太慢了.
Mayer 考虑的方案是定义一个函数 \[ f_{ij}:=\exp(-\beta\phi(r_{ij}))-1 \] 则可以对\(f\)作展开 \[ \begin{aligned} Q_N&=\frac{1}{N!}\int\prod_id^3\vec{r}_i\prod_{j<k}(1+f_{jk}) \\&= \frac{1}{N!}\int\prod_id^3\vec{r}_i\left[1+\sum_{j<k}f_{jk}+\sum_{j<k,l<m}^{(j,k)\ne(l,m)}f_{jk}f_{lm}+\cdots \right] \end{aligned} \] \(N\)个粒子按编号, 可以形成\(C_N^2\)个无序数对, 上面各项是无序数对的排列
\(0\)个数对排列: 只有一种排列, 并且含零个数对, 因此是\(1\).
\(1\)个数对排列: 含一个数对, 因此是\(f_{jk}\); 同时用求和包含所有可能的排列.
\(2\)个数对排列: 含两个数对, 因此是\(f_{jk}f_{lm}\); 同时用求和包含所有可能的排列.
...
Mayer 集团展开
一种更为几何(图论)的方法是作图. 把\(N\)个编号写出, 积分核可以拆成很多单项式, 每一项中的一个\(f_{ij}\)因子可以用点\(i\)到点\(j\)的连线表示, 这样一项和一张图一一对应. 例如, 下图展示了\(N=8\)的两张图. 上子图表示项\(f_{34}f_{68}\)的积分, 下子图表示项\(f_{12}f_{14}f_{67}\)的积分.
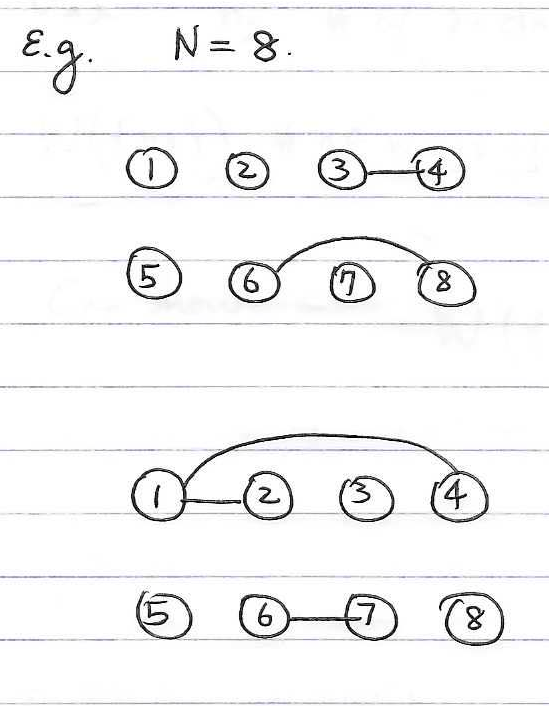
事实上, 从图中可以看出的是, 图并非最小的单元结构. 图中还有更小的单元结构, 即按照联通性区分的各个子图, 我们通常称之为 集团. 显然, 一个集团的积分值不依赖于标号本身, 只依赖于集团的拓扑结构. 如果我们把这个拓扑结构记作\(c\), 并且定义
集团积分 \[ b_c:=\frac{1}{n_c!V}\int\prod_{i=1}^{n_c}d^3\vec{r}_i\cdot\prod_{p\in c}f_p \]
其中, \(n_c\)表示集团\(c\)中的点的个数, 这样定义对后面有方便; \(p\)表示集团中存在的数对, 对\(p\)的连乘就是集团涉及的所有\(f\)项. 任何单张图总能分解为集团的乘积. 假设一张图中, 集团\(c\)出现\(m_c\)次, 则对应积分为\((n_c!Vb_c)^{m_c}\). 但问题在于, 全套\(\{m_c\}\)相同的图不止一张.
最简单地, 考虑\(N=3\)系统, 只有\(1,2\)相连或者只有\(1,3\)相连是两张图, 但它们都只有一个单粒子集团和一个双粒子集团.
如果考虑\(W(\{m_c\})\)是这套\(\{m_c\}\)对应的图张数, 则位形积分可以写为 \[ Q_N=\sum_{\{m_c\}}'\frac{W(\{m_c\})}{N!}\prod_c(Vn_c!b_c)^{m_c} \] 带 prime 的求和仍是表示约束\(\sum_{c}m_cn_c=N\). \(W(\{m_c\})\)实际上是不难求的. 全排列为\(N!\), \(m_c\)个集团\(c\), 每个集团的内部交换数为\(n_c!\), 集团间的交换数为\(m_c!\), 因此 \[ W(\{m_c\})=\frac{N!}{\prod_cm_c!(n_c!)^{m_c}} \] 从而求出位形积分为 \[ Q_N=\sum_{\{m_c\}}'\prod_c\frac{(Vb_c)^{m_c}}{m_c!} \]
另一种集团展开表示
上面的集团展开是很"纯粹的"集团, 按照集团求和. 求和时应当注意, 不同拓扑结构的集团可能具有相同的粒子数.
例如\(N=3\)集团, \(1,2\)和\(1,3\)分别相连是一种拓扑结构, 这个集团内包含两个\(f\)项; 三个点两两相连是另一种拓扑结构, 这个集团内包含三个\(f\)项.
有时候, 我们希望按照不同的粒子数求和, 每个粒子数可能对应一种集团, 也可能对应多种. 因此, 需要把\(c\)进行一定合并, 形成对\(l\)的求和或者连乘.
从比较简单的情形开始考虑, 假设集团\(c\)和集团\(s\)的粒子数都为\(l\), 并且其它集团粒子数都不为\(l\). 则 \[ Q_N=\sum_{\{m_a\}}^{a\neq c,s}\sum_{m_c+m_s}\sum_{m_c,m_s}'\frac{(Vb_c)^{m_c}}{m_c!}\frac{(Vb_s)^{m_s}}{m_s!}\prod_{a}^{a\neq c,s}\frac{(V b_a)^{m_a}}{m_a!} \] 这里用\(a\)表示任意其它集团. 约束条件现在只对\(m_c,m_s\)的求和成立: \[ \sum_am_an_a+m_cl+m_sl=N \] 总之, 约束条件表明, 若先对\(c,s\)求和, 则\(m_c,m_s\)之和为定值(以后还要对定值取一定的值并求和). 这种约束对于先把\(c,s\)的和项求出是有利的, 因为二项式定理为 \[ (x+y)^{m_c+m_s}=\sum_{m_c,m_s}'\frac{(m_c+m_s)!}{m_c!m_s!}x^{m_c}y^{m_s} \] 因此容易写出对\(c,s\)的求和, 位形积分改写为 \[ Q_N=\sum_{\{m_a\}}^{a\ne c,s}\sum_{m_c+m_s}\frac{[V(b_c+b_s)]^{(m_c+m_s)}}{(m_c+m_s)!}\prod_{\{m_a\}}^{a\ne c,s}\frac{(V b_a)^{m_a}}{m_a!} \] \(m_c+m_s\)实际上就是所有\(l\)个粒子的集团总数, 可以记作\(m_l\), 它不应与\(m_c\)混淆, 因为已经对集团结构\(c\)(或者\(s\), \(a\))和粒子数\(l\)采用了不同的记号; \(b_c+b_s\)也对应着所有\(l\)个粒子的可能拓扑结构的贡献.
读者不难发现, 这个推导过程容易推广到任何情况, 以至于可以把所有对拓扑结构的求和改写为对\(l\)的求和: \[ Q_N=\sum_{\{m_l\}}'\prod_l\frac{(Vb_l)^{m_l}}{m_l!} \] 有时候, 也常把\(b_l\)中的系数\(l!\)提出:
\(l\)-集团的集团积分 \[ b_l:=\frac{1}{V}\int\prod_{i=1}^ld^3\vec{r}_i\sum_{c\in C_l}\prod_{p\in c}f_{p} \] 则位形积分写为 \[ Q_N=\sum_{\{m_l\}}'\prod_l\frac{1}{m_l!}\left(\frac{Vb_l}{l!}\right)^{m_l} \]
其中, \(C_l\)表示\(l\)-集团的集合族, \(c\)表示\(C_l\)中的一个集团, \(p\)表示\(c\)中的一个数对.