数值解和优化问题(04):基于梯度的多元函数优化
上一节绕过求导数直接对函数优化, 可以看到还是比较复杂的, 而本节打算从最理想的二次型出发, 基于函数的导函数来研究优化问题, 因为二次型的形式比较简单: \[ f_{p}(\boldsymbol{x})=f_p(\boldsymbol{x}_0)-\boldsymbol{b}^{\mathbf{T}}\cdot(\boldsymbol{x}-\boldsymbol{x}_0)+\frac{1}{2}(\boldsymbol{x}-\boldsymbol{x}_0)^{\mathbf{T}}\mathbf{A}(\boldsymbol{x}-\boldsymbol{x}_0) \] 即二次型是一种一二阶导都是常量且高阶导数为零的同时, 还可优化的函数. 不失一般性, 对于函数\(f\in \mathbb{C}^{2}\), 平移初始位置和函数值的零点, 使得它总能写成形如 \[ f(\boldsymbol{x})=-\boldsymbol{b}^\mathbf{T}\cdot\boldsymbol{x}+\frac{1}{2}\boldsymbol{x}^\mathbf{T}\mathbf{A}\boldsymbol{x}+o(|\boldsymbol{x}|^2) \] 的形式. \(\boldsymbol{b}\)和\(\mathbf{A}\)分别给定\(f(\boldsymbol{x})\)在原点的一阶和二阶偏导数. 还可以定义 残差: \[ \begin{aligned} \boldsymbol{r}(\boldsymbol{x}) &= -\boldsymbol{\nabla} f(\boldsymbol{x}) \\ \text{对于上述平移}&\text{过的函数式, 有} \\ \boldsymbol{r}(\boldsymbol{x}) &\approx \boldsymbol{b}-\mathbf{A}\boldsymbol{x} \end{aligned} \] 现在我们从原点出发, 希望对函数进行优化.
最速下降法
最速下降法的逻辑十分简单: 在一个点附近最好的局部优化方向自然是负梯度方向, 即残差方向: \[ \boldsymbol{x}_{k+1}=\boldsymbol{x}_k+\lambda_k\boldsymbol{r}_k \] 其中\(\lambda_k\)是个待定参数, 它自身构成一维优化问题, 因为: \[ \phi_k(\lambda_k):=f(\boldsymbol{x}_k+\lambda_k\boldsymbol{r}_k) \] 像这样反复迭代, 最终加上一定的结束条件即可.
共轭梯度法
上面的最速下降法类似一种贪心策略, 通过一系列局部最优达到整体的最优, 但是很多时候, 局部最优并不导向整体最优, 或者处处进行局部优化并不是很高效的方案. 如果函数的二阶导数在某些方向比较奇葩, 例如相较于其他方向而言具有特别大的数值, 在这样复杂的地形中优化函数的时候, 如果按照最陡下降法来做就会沿着一个多重曲折的折线行进. 这样的效果是需要很多小碎步才能接近极小值, 因此实际上是效率很低的.
请看下面的函数, 它是著名的 Rosenbrock 函数, 使用最速下降法进行优化, 竟然整整迭代了1000次, 这多少有些超出了我们的接受范围.
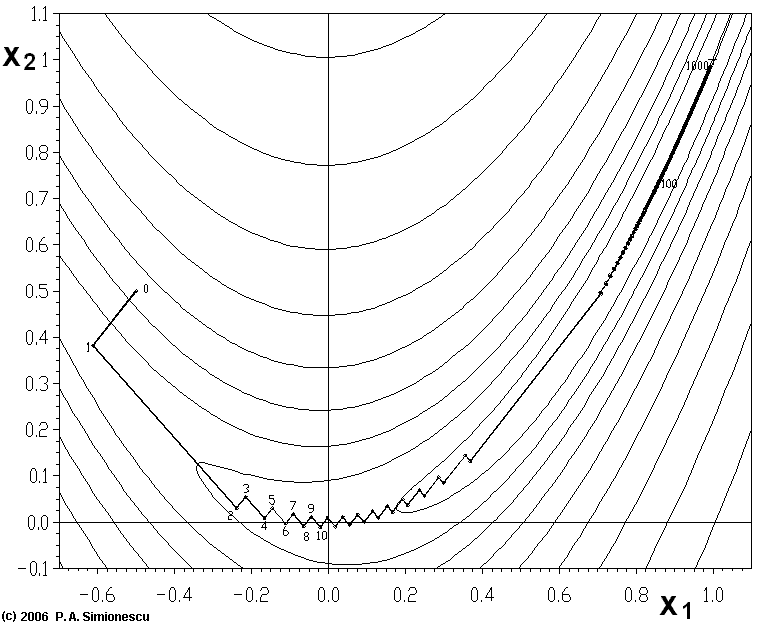
为什么会造成这样的结果? 因为最速下降法的两次线搜索的位移是正交的, 这其实一定程度上破坏了搜索的成果. 如果引入参数, 确保搜索方向\(\boldsymbol{p}_i\)并不是只依赖于负梯度\(\boldsymbol{r}_i\), 而是 \[ \boldsymbol{p}_i=\boldsymbol{r}_i+\beta_{i-1}\boldsymbol{p}_{i-1} \] 位置的递推式为 \[ \boldsymbol{x}_{i+1}=\boldsymbol{x}_i+\alpha_i\boldsymbol{p}_i \] \(\alpha_i\)可以用一维优化来求出, \(\beta_i\)可以证明具有形式 \[ \beta_i=\frac{\boldsymbol{r}_{i+1}^\mathbf{T}\boldsymbol{r}_{i+1}}{\boldsymbol{r}_i^\mathbf{T}\boldsymbol{r}_i} \]
步骤
给定\(\boldsymbol{p}_0=\boldsymbol{r}_0=-\displaystyle\boldsymbol{\nabla} f(\boldsymbol{x}_0)\), \(k=0\)
根据 \[ \phi(\alpha_k):= f(\boldsymbol{x}_k+\alpha_k\boldsymbol{p}_k) \] 进行一维优化. 对于二次型可以直接利用公式计算\(\alpha_k\) \[ \alpha_k=\frac{\boldsymbol{p}_k^\mathbf{T}\boldsymbol{r}_k}{\boldsymbol{p}_k^\mathbf{T}\mathbf{A}\boldsymbol{p}_k} \]
更新位置和残差: \[ \begin{aligned} \boldsymbol{x}_{k+1}&=\boldsymbol{x}_k+\alpha_k\boldsymbol{p}_k \\ \boldsymbol{r}_{k+1}&=-\boldsymbol{\nabla} f(\boldsymbol{x}_{k+1})\qquad(\text{一般形式}) \\ &=\boldsymbol{r}_k-\alpha_k\mathbf{A}\boldsymbol{p}_k\qquad(二次型) \end{aligned} \]
判定循环终止条件, 如果满足即跳出循环, 否则继续.
更新搜索方向 \[ \begin{aligned} \beta_k&=\frac{\boldsymbol{r}_{k+1}^\mathbf{T}\boldsymbol{r}_{k+1}}{\boldsymbol{r}_k^\mathbf{T}\boldsymbol{r}_k} \\ \boldsymbol{p}_{k+1}&=\boldsymbol{r}_{k+1}+\beta_k\boldsymbol{p}_k \end{aligned} \]
\(k\)递增\(1\), 将新的\(k,\boldsymbol{x}_k,\boldsymbol{p}_k,\boldsymbol{r}_k\)带到步骤1迭代.