函数数值计算(03):Chebyshev 多项式近似
很多的函数是以级数的形式表达的, 比如 Bessel 函数, Legendre 函数. 级数展开在数学上是收敛的, 但是直接按照级数去计算往往并不是最合适的方法, 例如
\[ \arctan x=x-\frac{1}{3}x^3+\frac{1}{5}x^5-\cdots\ ,\ x\in[-1,1] \]
利用这个展开式计算\(\arctan1\), 即\(\displaystyle\frac{\pi}{4}\), 收敛速度慢得离谱. 我们介绍一种新的展开方式.
Chebyshev 多项式及其基本性质
Chebyshev 多项式 定义为 \[ T_n(x)=\cos(n\arccos x)\ ,\ x\in[-1,1] \]
引入辅助角\(x=\cos\phi\), 得到一个正交归一关系
\[ \int_{0}^\pi T_i(\cos\phi)T_j(\cos\phi)d\phi=\frac{\pi}{2}(1+\delta_{0i})\delta_{ij} \]
用\(x\)表达:
\[ \int_{-1}^1 \frac{T_i(x)T_j(x)}{\sqrt{1-x^2}}dx=\begin{aligned}\begin{cases}\displaystyle 0&\text{if }i\ne j \\\displaystyle \frac{\pi}{2}&\text{if }i=j\ne0 \\\displaystyle \pi&\text{if }i=j=0 \end{cases}\end{aligned} \]
零点处的正交归一关系
在\([-1,1]\)上的正交归一关系提示我们将其用作函数展开的基: \[ f(x)=\frac{c_0}{2}+\sum_{k=1}^{N-1}c_kT_k(x) \]
如果希望这个式子在\(T_N(x)\)的零点处严格成立, 则
\[ f\left[\cos((k+\frac{1}{2})\pi/N)\right]=\frac{c_0}{2}+\sum_{m=1}^{N-1}c_m\cos((k+\frac{1}{2})m\pi/N) \] 我们先考虑两个特别的求和式.
1. \(\displaystyle\sum_{k=0}^{N-1}\cos((k+\frac{1}{2})\theta)\)
这个式子没啥好说的, 凑一个因子\(\sin(\theta/2)\), 得 \[ \begin{aligned} \sum_{k=0}^{N-1}\cos((k+\frac{1}{2})\theta)&= \frac{1}{\sin\theta/2}\sum_{k=0}^{N-1}\cos((k+\frac{1}{2})\theta)\sin\theta/2 \newline&= \sum_{k=0}^{N-1}\frac{\sin(k+1)\theta-\sin k\theta}{2\sin\theta/2} \newline&= \frac{\sin(N\theta)}{2\sin\theta/2} \end{aligned} \]
2. \(\displaystyle\sum_{k=0}^{N-1}\cos((k+\frac{1}{2})m\pi/N)\cos((k+\frac{1}{2})m'\pi/N)\)
同样进行积化和差 \[ \begin{aligned} \text{原式}&= \frac{1}{2}\sum_{k=0}^{N-1}\cos((k+\frac{1}{2})(m+m')\pi/N)+\frac{1}{2}\sum_{k=0}^{N-1}\cos((k+\frac{1}{2})(m-m')\pi/N) \newline&= \frac{\sin(m+m')\pi}{4\displaystyle\sin\frac{m+m'}{2N}\pi}+\frac{\sin(m-m')\pi}{4\displaystyle\sin\frac{m-m'}{2N}\pi} \end{aligned} \] 简单地讨论\(m\)和\(m'\)的取值, 得到 \[ \sum_{k=0}^{N-1}\cos((k+\frac{1}{2})m\pi/N)\cos((k+\frac{1}{2})m'\pi/N)=\begin{aligned}\begin{cases}\displaystyle 0&\text{if }m\ne m' \newline\displaystyle \frac{N}{2}&\text{if }m=m'\ne0 \newline\displaystyle N&\text{if }m=m'=0 \end{cases}\end{aligned} \] 记作\(T_{mm'}\).
Chebyshev 展开
回到系数满足的条件 \[ f\left[\cos((k+\frac{1}{2})\pi/N)\right]=\frac{c_0}{2}+\sum_{m=1}^{N-1}c_m\cos((k+\frac{1}{2})m\pi/N) \] 两边同乘以\(\displaystyle\cos((k+\frac{1}{2})m'\pi/N)\)并对\(k\)求和, 得到 \[ \sum_{k=0}^{N-1}f\left[\cos((k+\frac{1}{2})\pi/N)\right]\cos((k+\frac{1}{2})m'\pi/N) =\frac{c_0}{2}T_{0m'} +\sum_{m=1}^{N-1}c_mT_{mm'}=\frac{N}{2}c_0\delta_{0m'} +\frac{N}{2}c_{m}\delta_{mm'} \] 取\(m'\)为\([0,N-1]\)上不同的整数, 得到 \[ \boxed{c_m=\frac{2}{N}\sum_{k=0}^{N-1}f\left[\cos((k+\frac{1}{2})\pi/N)\right]\cos((k+\frac{1}{2})m\pi/N)} \] 这就是 Chebyshev 展开的系数计算公式.
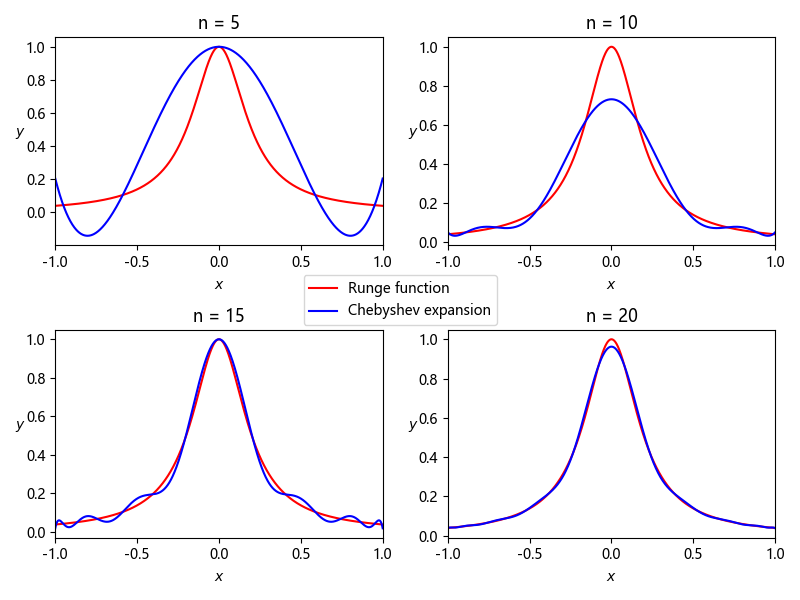
这里给出 Chebyshev 展开在 Runge 现象中的应用, 它的各个基之间是正交的, 而幂级数的基之间具有很大的overlap, 所以前者才能解决所谓的 Runge 现象.