函数数值计算(01):多项式插值
Lagrange 插值法
考虑区间\([x_0,x_n]\)上的n次多项式内插
\[ P_n(x)=a_0+a_1x+\cdots+a_nx^n \]
已知的点为\((x_0,y_0),(x_1,y_1),\cdots,(x_n,y_n)\). 内插要求多项式的曲线通过这些点:
\[ P_n(x_j)=y_j\ ,\ j = 0, 1, \cdots, n \]
为了求出这个问题的一般解, 我们将\(P_n\)写成多项式的和:
\[ P_n(x) = \sum_jp_{nj}(x) \]
其中, \(p_{nj}(x_k)=y_j\delta_{jk}\).
由于\(p_{nj}\)具有\(n\)个零点, 故它必然能写成
\[ p_{nj}(x)=a_{nj}\prod_{m=0且m\ne j}^{n}(x-x_m) \]
\(a_{nj}\)只是系数, 因为\(n\)个零点已经构成了\(n\)次多项式. 代入\((x_j, y_j)\)得到
\[ a_{nj}=\frac{y_j}{\prod_{m=0且m\ne j}^{n}(x_j-x_m)} \]
最终我们得到
\[ \boxed{P_n(x)=\sum_jy_jL_j(x)} \newline \ \newline \text{其中, } \boxed{L_j(x)=\prod_{m\ne j}\frac{x-x_m}{x_j-x_m}} \]
这个结果被称作 Lagrange多项式, 也称 Lagrange内插公式.
Newton 插值法
Newton 的多项式内插法是一种递推方法:
\[ N(x)=\sum_{j=0}^{n}a_jn_j(x) \newline\text{其中, } n_j(x)=\prod_{k=0}^{j-1}(x-x_k),\ n_0(x)=1 \]
好处是如果增加一个支撑点, 不破坏之前所有支撑条件, 仅需计算\(a_{n+1}\)和\(n_{n+1}(x)\):
\[ a_0+\sum_{j=1}^{n+1}a_j\cdot\prod_{k=0}^{j-1}(x_{n+1}-x_k) = y_{n+1} \]
如何求解系数呢? 上式相当于一个方程组
\[ \begin{pmatrix} 1 & 0 & 0 & \cdots & 0\\ 1 & x_1-x_0 & 0 & \cdots & 0\\ 1 & x_2-x_0 & (x_2-x_0)(x_2-x_1) & \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & 0\\ 1 & x_n-x_0 & (x_n-x_0)(x_n-x_1) & \cdots & \prod_{j=0}^{n-1}(x_n-x_j) \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ \cdots \\ a_n \end{pmatrix} = \begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ \cdots \\ y_n \end{pmatrix} \]
解这个下三角矩阵描述的线性方程组问题, 即得各项系数.
Neville 迭代法
先构造\(n+1\)个常数函数:
\[ Q_i(x)=y_i \]
按指标大小顺序排列\(Q_i\), 再用每对相邻的函数构造更高阶函数, 并且用双下标做记号:
\[ P_{ij}=\frac{(x-x_i)Q_j-(x-x_j)Q_i}{x_j-x_i} \]
现在得到\(n\)个双下标的一次函数, 按第一指标顺序排列, 再用相邻的函数对构造二次函数:
\[ P_{ijk}=\frac{(x-x_i)P_{jk}-(x-x_k)P_{ij}}{x_k-x_i} \]
至于下标, 略去重复数字, 为三下标. 如法炮制, 最终得到单个\(n\)次函数.
Runge 现象
一般情况下, 多项式的次数越多, 需要的数据就越多, 而预测也就越准确. 但也存在插值次数越高, 插值结果越偏离原函数的现象, 特别常发生在区间的端点处, 称为 Runge 现象[1].
特别地, 考虑函数
\[ f(x)=\frac{1}{1+25x^2} \]
称为 Runge 函数. 在区间\([-1, 1]\)上, 以\(\frac{2}{n}\)为步长选取支撑点进行 Lagrange 插值, 得到的结果如下所示:
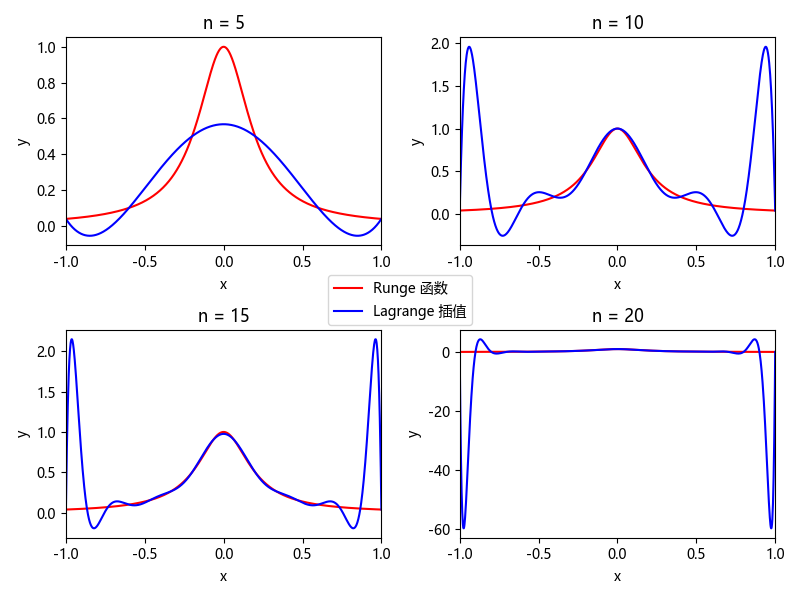
造成这种现象的主要原因是,拉格朗日插值使用的函数基组\(1,𝑥,𝑥^2,\cdots\)并不是正交基, 插值结果十分病态, 可以考虑对基函数进行 Schmidt 正交化, 但更方便的方案是选取既正交又简单的非多项式基, 或者干脆不使用这种内插方案, 这是下一节将要讨论到的.